Introduction
The concept of the present value of an annuity is a fundamental financial tool used in various fields such as finance, investment, and retirement planning. It allows individuals and businesses to assess the current worth of a series of future cash flows or payments. In this article, we will delve into the concept of the present value of an annuity, its formulas, and practical examples.What is an Annuity?
An annuity is a financial arrangement involving equal payments or cash flows made or received at regular intervals. These intervals can be monthly, quarterly, annually, or any other consistent timeframe. Annuities are commonly used for various purposes, including retirement savings, loan repayments, and insurance policies. Annuities are a fundamental financial instrument that plays a crucial role in personal finance, retirement planning, and investment strategies. In essence, they represent a series of regular payments made or received at consistent intervals. This article explores annuities in detail, focusing on their definition, types, and the concept of calculating the present value of annuities, particularly when considering them 25 times consecutively.What is an Annuity?
- Regular Payments: At its core, an annuity involves a stream of periodic payments. These payments can be equal in size and occur at predetermined intervals. The intervals may be monthly, quarterly, annually, or any other set timeframe.
- Common Applications: Annuities have diverse applications, making them an essential financial tool. They are frequently used in scenarios such as retirement planning, insurance, and managing loans.
- Contractual Agreements: Annuities are often established through contractual agreements. In many cases, an individual invests a lump sum or makes periodic contributions into an annuity, and in return, they receive regular payments for a specific period or for the rest of their life, depending on the type of annuity.
Types of Annuities:
-
Fixed Annuities:
- Offer fixed, predetermined payments at regular intervals.
- Provide stability and predictability in income.
-
Variable Annuities:
- Payments fluctuate based on the performance of underlying investments, typically mutual funds.
- Offer the potential for higher returns but come with investment risks.
-
Immediate Annuities:
- Payments begin almost immediately after the initial investment.
- Useful for retirees seeking an immediate income stream.
-
Deferred Annuities:
- Payments begin at a future date, allowing for tax-deferred growth.
- Commonly used for retirement planning.
-
Lifetime Annuities:
- Payments continue for the recipient's lifetime, ensuring income security.
-
Fixed Period Annuities:
- Payments occur for a specified number of years, regardless of the recipient's longevity.
Calculating the Present Value of Annuities:
- The Concept: The present value (PV) of an annuity is a vital financial concept that determines the current worth of a series of future payments. Calculating the PV helps individuals and businesses assess the current value of cash flows, which may have different purchasing power due to factors like inflation or varying interest rates.
- Formula for PV: The formula to calculate the present value of an annuity depends on whether it's an ordinary annuity or an annuity due. For an ordinary annuity, the formula is:
Where:
PV = PMT x [(1 - (1 + r)^(-n)) / r]- PV is the present value of the annuity.
- PMT represents the periodic payment.
- r is the interest rate per period.
- n denotes the total number of periods.
- Calculating PV 25 Times: To calculate the PV of an annuity 25 times consecutively, you would perform the PV calculation individually for each set of cash flows or payments. This means applying the annuity formula 25 times, using the appropriate values for each specific set of payments and intervals.
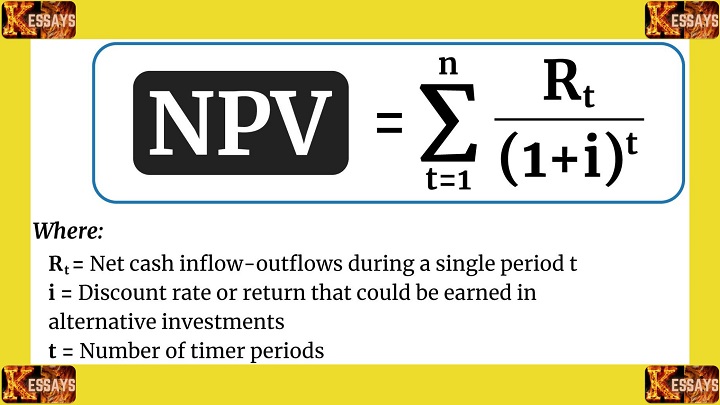
Read Also: Net Present Value Assignment: Calculation, Formulas, and Examples
The Importance of Present Value
The present value (PV) of an annuity is crucial because it helps individuals and businesses make informed financial decisions. By calculating the PV of an annuity, you can determine the current value of a stream of future payments, which may have different purchasing power due to factors like inflation or varying interest rates. The concept of present value (PV) is a fundamental financial tool that plays a vital role in helping individuals and businesses make informed financial decisions. Particularly, when dealing with annuities, understanding the PV is essential to assess the current value of future payments. In this article, we explore the significance of present value, emphasizing its role in financial decision-making.The Role of Present Value:
-
Determining Current Value:
- PV is instrumental in determining the current worth of a series of future payments or cash flows. This is invaluable when assessing the value of assets, investments, or financial obligations.
-
Considering Time Value of Money:
- The concept of time value of money recognizes that money today is worth more than the same amount in the future. PV accounts for this principle by discounting future cash flows to their current value.
-
Factoring in Inflation:
- Inflation erodes the purchasing power of money over time. Calculating the PV helps adjust for the impact of inflation, enabling a more accurate assessment of an investment's real value.
-
Dealing with Varying Interest Rates:
- Interest rates can change over time, affecting the value of future cash flows. PV takes into account the prevailing interest rate to determine the current value accurately.
-
Assessing Investment Opportunities:
- When evaluating investment opportunities, individuals and businesses use PV to compare the potential returns of different projects. It helps identify which investments are more lucrative in today's terms.
The Importance in Annuities:
-
Retirement Planning:
- In retirement planning, knowing the PV of future pension payments or annuities is crucial. It helps retirees gauge the adequacy of their retirement income and make necessary adjustments.
-
Loan and Debt Management:
- For borrowers, understanding the PV of loan repayments aids in budgeting and long-term financial planning. It allows them to assess the true cost of borrowing.
-
Insurance Planning:
- Insurance companies use PV to calculate policy premiums and determine appropriate payouts. Policyholders can use PV to assess the value of their insurance coverage.
-
Business Valuation:
- Businesses employ PV to value future cash flows, such as expected revenue or expenses. It is integral to assessing a company's overall financial health.
 In conclusion, the importance of present value cannot be overstated in the realm of financial decision-making. It helps individuals and businesses navigate complex financial landscapes, account for time value of money, and make informed choices about investments, loans, and retirement planning. Calculating the PV of annuities, especially when considering them 25 times consecutively, offers precision and clarity in financial assessments, ultimately leading to better financial outcomes.
In conclusion, the importance of present value cannot be overstated in the realm of financial decision-making. It helps individuals and businesses navigate complex financial landscapes, account for time value of money, and make informed choices about investments, loans, and retirement planning. Calculating the PV of annuities, especially when considering them 25 times consecutively, offers precision and clarity in financial assessments, ultimately leading to better financial outcomes.
Calculating the Present Value of an Annuity
The present value of an annuity can be calculated using specific formulas, depending on whether it is an ordinary annuity or an annuity due. Let's explore both scenarios:1. Present Value of an Ordinary Annuity (PV)
The formula for the present value of an ordinary annuity is:PV = PMT x [(1 - (1 + r)^(-n)) / r]
- PV is the present value of the annuity.
- PMT represents the periodic payment.
- r is the interest rate per period.
- n denotes the total number of periods.
2. Present Value of an Annuity Due (PV)
An annuity due is slightly different because payments occur at the beginning of each period. To calculate its PV, you can use the same formula as for the ordinary annuity but multiply it by (1 + r) since payments occur at the beginning of each period:PVDue = PMT x [(1 - (1 + r)^(-n)) / r] x (1 + r)
Example Calculation
Let's calculate the present value of a simple annuity. Suppose you have ₱ 5,000.00 payable semiannually for 10 years, and the interest rate is 6%, compounded semiannually:- PMT = ₱ 5,000.00
- r = 6% or 0.06 per semi-annual period
- n = 10 years * 2 (semi-annual payments) = 20 semi-annual periods
PV = PMT x [(1 - (1 + r)^(-n)) / r]
Where:
PV = Present Value of the annuity
PMT = Payment amount (₱ 5,000.00 in this case)
r = Interest rate per semi-annual period (0.06)
n = Total number of semi-annual periods (20)
Using the formula for the present value of an ordinary annuity:
PV = ₱5,000 × [(1 - (1 + 0.06/2)^(-20)) / (0.06/2)]
PV ≈ ₱5,000 × 14.87793 ≈ ₱74,389.65
So, the present value of the annuity is approximately ₱ 74,389.65.
Present Value of Other Annuities
The concept of present value (PV) plays a pivotal role in financial decision-making. It allows individuals and businesses to determine the current worth of a stream of future payments or cash flows. While we've discussed the PV of an ordinary annuity in detail, this article delves into other scenarios where PV calculations are vital. We'll explore calculating the PV of various annuities, including annuities with different payment schedules, amounts, and timeframes.Present Value of an Annuity of Rs 3,000 for 15 Years
- Scenario: Imagine you have an annuity that offers Rs 3,000 payable annually for a period of 15 years.
- Formula: To calculate the PV of this specific annuity, you can use the same formula as for an ordinary annuity but with values specific to this scenario:
Where:
PV = PMT × [(1 - (1 + r)^(-n)) / r]- PMT = Rs 3,000 (annual payment)
- r = Interest rate per year
- n = Total number of years (15)
- Calculation: Input the values into the formula to find the PV.
- Significance: This calculation helps you assess the current value of the annuity's future payments in this specific context.
Using a Basic Calculator for PV of Ordinary Annuity
- Scenario: Not everyone has access to specialized financial software. In such cases, you can use a basic calculator to calculate the PV of an ordinary annuity manually.
- Formula: The formula for the PV of an ordinary annuity is:
PV = PMT × [(1 - (1 + r)^(-n)) / r]- PMT: Payment amount
- r: Interest rate per period
- n: Total number of periods
- Calculation: Input the values into your calculator, following the formula step by step.
- Significance: This method provides a practical way to calculate PV without relying on specialized financial software or spreadsheets.
Present Value of a $600 Annuity Payment over 4 Years at 6% Interest
- Scenario: Consider an annuity with $600 payable quarterly for a period of 4 years, with an annual interest rate of 6%.
- Formula: Apply the ordinary annuity formula to this scenario, adjusting the values accordingly:
PV = PMT × [(1 - (1 + r)^(-n)) / r]- PMT: $600 (quarterly payment)
- r: Interest rate per quarter (6% / 4)
- n: Total number of quarters (4 years * 4 quarters per year)
- Calculation: Input the values into the formula to calculate the PV.
- Significance: This calculation aids in understanding the current value of the future cash flows in a context involving different payment frequencies and timeframes.
