Introduction
Game Theory, which is the study of strategic decision-making, goes far beyond mathematical puzzles or academic theory. It provides powerful tools for understanding how individuals, businesses, and even nations make choices when outcomes depend on the actions of others. From economics and politics to business strategy and biology, Game Theory reveals the dynamics of competition, cooperation, and negotiation in real-world scenarios.
For many students, however, Game Theory assignments can be challenging due to their mathematical rigor and interdisciplinary applications. That’s where professional Game Theory Assignment Help services come in. In this article, we’ll break down the essentials of Game Theory while also introducing trusted support platforms such as kessays.com, kector.com, kesity.com, and peachyessay.com. Whether you’re looking to strengthen your academic performance or simply explore this fascinating field, you’ll find practical insights and guidance here.

Understanding Game Theory
1.1 What is Game Theory?
Game Theory is the study of decision-making in situations where the outcome of one player’s choice depends not only on their own actions but also on the actions of others. These situations are called “games,” not because they are recreational, but because they have rules, strategies, and results that can be systematically analyzed.
Game Theory applies to many real-world contexts such as market competition, political negotiations, military strategies, auctions, and even the evolutionary behavior of animals.
At its core, Game Theory examines both conflict and cooperation. It explains how rational decision-makers:
-
evaluate the strategies available to them,
-
anticipate how others will act, and
-
select choices that maximize benefits or minimize risks.
This makes it a powerful framework for analyzing interactions where interests may align, clash, or overlap.
Key Components of Game Theory
To fully understand Game Theory, one must grasp its essential building blocks:
-
Players: The participants or decision-makers in the game. Players may be individuals (like two friends deciding where to eat), organizations (like competing firms), governments (engaging in diplomacy), or even species (in evolutionary biology).
-
Strategies: The set of actions or plans available to each player. A strategy can be as simple as a single decision (cooperate or defect in the Prisoner’s Dilemma) or a complex plan that unfolds over multiple stages (such as a long-term business strategy in repeated competition).
-
Payoffs: The outcomes or rewards each player receives depending on the strategies chosen by everyone involved. Payoffs can represent profits, utility, votes, survival advantages, or other measurable benefits. They highlight the consequences of different decision paths.
-
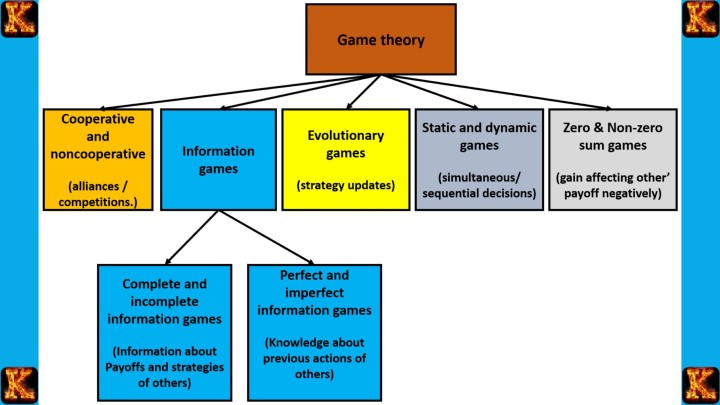
Information: The knowledge that players have about the game and about other players’ possible moves. Information can be:
-
Complete: Everyone knows the rules, strategies, and payoffs.
-
Incomplete: Some elements are unknown (e.g., hidden costs or private preferences).
-
Asymmetric: One player knows more than the other, giving them an advantage.
-
Together, these elements allow analysts to model real-world interactions and predict outcomes under various conditions.
Read Also: The Impact of UK Data Protection Laws on E-commerce
2. Core Concepts in Game Theory
These ideas form the backbone of game-theoretic analysis:
1. Rationality
Game Theory assumes players are rational, meaning they consistently choose actions that maximize their own payoff (utility, profit, or survival).
-
Example: In a business price war, each firm lowers prices only if it increases its long-term profits.
2. Dominant Strategy
A dominant strategy is one that yields the best payoff for a player no matter what others do.
-
If such a strategy exists, a rational player will always follow it.
-
Example: In the Prisoner’s Dilemma, “confess” is a dominant strategy because it gives a better outcome whether the other prisoner confesses or stays silent.
3. Best Response
A best response is the optimal strategy given what a player expects others to choose.
-
Unlike a dominant strategy, it depends on the opponent’s action.
-
Example: In Rock-Paper-Scissors, if you believe your opponent will play Rock, your best response is Paper.
4. Equilibrium
An equilibrium is a situation where no player can improve their payoff by changing their strategy alone. The most famous form is the Nash Equilibrium.
-
At equilibrium, every player is playing their best response to the others.
-
Example: In Cournot competition (two firms choosing output), both firms reach a production level where neither can gain by adjusting output unless the other also changes.
3. Key Equilibrium Concepts
1. Nash Equilibrium
The Nash Equilibrium is the foundation of Game Theory. It occurs when each player chooses a strategy that is the best response to the strategies of others. At this point, no player can improve their payoff by changing their decision unilaterally.
-
Example: In the Prisoner’s Dilemma, both confessing is a Nash Equilibrium because neither prisoner benefits from switching strategies alone.
2. Subgame Perfect Equilibrium (SPE)
The Subgame Perfect Equilibrium refines Nash Equilibrium for sequential or multi-stage games. It requires that players’ strategies form a Nash Equilibrium not just for the overall game, but for every possible subgame. This ensures credibility: players will only choose strategies they would realistically carry out at every stage.
-
Example: In bargaining or entry-deterrence games, SPE rules out “empty threats” (like a firm promising to retaliate with a strategy that would harm itself).
3. Mixed Strategy Equilibrium
A Mixed Strategy Equilibrium occurs when players randomize over available strategies rather than sticking to one choice. This makes opponents uncertain and prevents them from exploiting predictable behavior. In equilibrium, the randomization is calibrated so that opponents are indifferent between their possible responses.
-
Example: In Rock-Paper-Scissors, the equilibrium is to play Rock, Paper, and Scissors each with probability 1/3, making the opponent unable to gain an advantage.
Read Also: Applying System Dynamics in Carbon Credit Trading
4. Types of Games
1. Zero-Sum Games
In a zero-sum game, one player’s gain is exactly equal to the other’s loss. The total payoff across players is always constant. These games are purely competitive because one side can only benefit at the expense of the other.
-
Example: Poker, chess, or most sports matches where a winner’s gain equals the loser’s loss.
2. Non-Zero-Sum Games
In non-zero-sum games, players’ outcomes are not strictly opposed. Both can gain, both can lose, or one can gain more than the other. Cooperation or competition can influence whether the outcome is mutually beneficial.
-
Example: Trade negotiations where both countries can benefit from agreement, but both may also suffer if talks collapse.
3. Cooperative Games
In cooperative games, players can make binding agreements to coordinate strategies and maximize joint payoffs. The focus is often on how to distribute the collective gains fairly among participants.
-
Example: Companies forming a cartel to fix prices, then deciding how to share profits.
4. Non-Cooperative Games
In non-cooperative games, players make decisions independently without enforceable agreements. Outcomes depend on strategic interaction, and trust or self-interest drives behavior.
-
Example: Firms competing in a market without collusion.
5. Repeated Games
Repeated games are interactions that occur multiple times. Unlike one-shot games, repetition allows strategies such as reputation-building, trust, and punishment to emerge. Long-term relationships often encourage cooperation.
-
Example: Price competition between firms repeated every day; cooperation may emerge to avoid destructive price wars.
6. Bayesian Games
Bayesian games involve incomplete or asymmetric information, where players do not know everything about others (such as payoffs, strategies, or preferences). Instead, they assign probabilities to different possibilities and base their strategies on beliefs.
-
Example: Auctions, where bidders do not know how much others value the item but act based on estimated probabilities.

5. Classic Models (must-teach examples)
1. Prisoner’s Dilemma
The Prisoner’s Dilemma illustrates the conflict between individual rationality and collective benefit. Two players are better off if both cooperate, but each has an incentive to defect for personal gain. When both defect, the outcome is worse for both than if they had cooperated.
-
Key insight: Rational self-interest can lead to outcomes that are collectively suboptimal.
2. Stag Hunt
The Stag Hunt highlights coordination problems and the importance of trust. Two hunters can either cooperate to hunt a stag, which gives a high payoff only if both commit, or individually hunt rabbits, which gives smaller but guaranteed payoffs.
-
Key insight: Mutual cooperation yields the best outcome, but fear of betrayal can push players toward safer but less rewarding strategies.
3. Battle of the Sexes
This model represents negotiation when players prefer different outcomes but still value being together more than being apart. For example, a couple wants to spend the evening together, but one prefers football and the other prefers the opera.
-
Key insight: The game demonstrates how players resolve conflicts of interest and the role of coordination in reaching mutually acceptable solutions.
4. Ultimatum Game
In the Ultimatum Game, one player proposes how to divide a sum of money and the other player can accept or reject. If the responder rejects, both players get nothing. Although rationality suggests any positive offer should be accepted, in practice unfair offers are often rejected.
-
Key insight: Human behavior often incorporates fairness, equity, and emotion, showing limits of pure rationality.
5. Matching Pennies / Rock-Paper-Scissors
These games capture situations of pure conflict with no stable pure-strategy equilibrium. In Matching Pennies, one player wins if both coins match while the other wins if they differ. Similarly, in Rock-Paper-Scissors, each choice can be beaten by another. The equilibrium lies in mixed strategies, where players randomize to remain unpredictable.
-
Key insight: Strategic uncertainty and randomization can be optimal in competitive interactions.
Read Also: Writing a PhD Thesis Defense Paper
6. Applications of Game Theory
Game Theory is not just abstract mathematics; it provides practical tools for analyzing decision-making in diverse real-world contexts. By applying its models and concepts, we can better understand competition, cooperation, and strategy across multiple fields.
1. Economics
Economists use Game Theory to explain how firms and individuals behave in markets where decisions are interdependent.
-
Oligopolies: Competing firms anticipate rivals’ pricing and production strategies, leading to models like Cournot and Bertrand competition.
-
Auctions: Game Theory explains bidder strategies in different auction formats (e.g., first-price, second-price) and helps design efficient auction rules.
-
Market Entry: Firms must weigh the costs and risks of entering a market while anticipating incumbent reactions such as price wars or deterrence strategies.
2. Politics
Political scientists apply Game Theory to understand power struggles, cooperation, and decision-making among states, parties, or voters.
-
Voting Systems: Strategic voting and coalition formation reveal how individuals or groups can influence outcomes.
-
International Treaties: Countries use Game Theory to decide whether to cooperate on issues like climate agreements or trade deals.
-
Arms Races: The dynamics of escalation and deterrence resemble zero-sum and prisoner’s dilemma-type models.
3. Business
In corporate strategy, Game Theory helps firms anticipate competitors’ moves and design winning strategies.
-
Pricing Strategies: Businesses decide whether to compete aggressively or cooperate tacitly to avoid price wars.
-
Competition: Firms evaluate moves such as product launches, advertising campaigns, or technology investments by predicting rival reactions.
-
Negotiation: Game Theory provides tools to analyze bargaining, contracts, and partnerships where incentives may align or diverge.
4. Biology
Biologists use evolutionary Game Theory to study how behaviors and traits survive over time.
-
Evolutionary Stable Strategies (ESS): These are strategies that, once adopted by a population, cannot easily be replaced by alternative strategies. Examples include cooperation, aggression, or altruism among species.
-
Animal Behavior: From mating rituals to territorial disputes, Game Theory explains how strategies evolve to maximize survival and reproduction.
5. Everyday Life
Game Theory is also useful in ordinary decision-making.
-
Traffic Routes: Drivers choose routes while anticipating congestion from others making similar choices.
-
Splitting Bills: Friends decide how to divide costs fairly while balancing individual incentives.
-
Social Interactions: Even small choices, like when to reply to a text, can reflect strategic timing and expectations about others’ reactions.
7. Limitations of Game Theory
While Game Theory is a powerful tool for analyzing strategic interactions, it also has important limitations that students and practitioners must recognize. These boundaries help us understand where Game Theory is most effective and where it may fall short.
1. Assumption of Rationality
Most Game Theory models assume that players are fully rational and will always act to maximize their payoffs. In reality, people often make decisions based on emotions, habits, or biases rather than strict rationality. For example, individuals may reject unfair offers in the Ultimatum Game even though accepting them would yield a higher payoff.
2. Dependence on Accurate Information
The predictions of Game Theory rely heavily on what players know about the game, their opponents, and potential payoffs. If information is incomplete, inaccurate, or asymmetric, outcomes may differ drastically from theoretical predictions. This is especially true in real-world negotiations, markets, or political settings where players may bluff, withhold, or misrepresent information.
3. Influence of Human Factors
Game Theory often abstracts away psychological, cultural, and social dynamics. In practice, decisions are shaped by trust, fairness, ethics, or cultural norms that cannot always be captured in mathematical models. For instance, cooperation in repeated games may arise not only from strategic calculation but also from moral values or long-term relationships.
Read Also: Nurses’ Role in Healthcare Capital Budgeting
Game Theory Assignment Help Services
Because Game Theory can be mathematically intensive and conceptually complex, many students turn to professional assignment help services for guidance. These services are designed to provide reliable support while ensuring academic integrity. In this article, we break down the essentials of Game Theory while also introducing trusted support platforms such as kessays.com, kector.com, myhomeworkhelp.com, and peachyessay.com. Whether you’re looking to strengthen your academic performance or simply explore this fascinating field, you’ll find practical insights and guidance here.
How They Work
-
Assignment Submission: Students upload their task with requirements and deadlines.
-
Review: Experts assess the scope, topic, and instructions.
-
Matching: The assignment is assigned to a qualified Game Theory specialist.
-
Completion: The expert prepares the solution according to academic standards.
-
Quality Check: The work is reviewed for accuracy, clarity, and originality.
-
Delivery: The completed assignment is returned on or before the deadline.
Benefits of Using Assignment Help
-
Expert Guidance: Access knowledge from professionals with deep expertise in Game Theory.
-
Time Efficiency: Save valuable time for other coursework, exams, or personal commitments.
-
Higher Grades: Well-prepared assignments often result in improved academic performance.
-
Originality: Trusted services guarantee plagiarism-free work tailored to your needs.
-
24/7 Support: Many platforms provide around-the-clock assistance to address student queries.
Choosing the Right Service
When selecting a Game Theory Assignment Help provider, consider the following:
-
Reputation: Look for services with proven experience, strong academic credibility, and positive reviews. Platforms such as kessays.com, kector.com, kesity.com, and peachyessay.com are well-regarded for their quality.
-
Confidentiality and Originality: Ensure the service protects your privacy and delivers plagiarism-free assignments.
-
Timely Delivery: Select providers known for consistent on-time submissions, as punctuality is crucial for avoiding academic penalties.
