Introduction
In the realm of finance, understanding the concept of the present value of future cash flows is pivotal for making informed investment decisions. This technique, rooted in the Time-Value of Money (TVM) principle, enables individuals and businesses to assess the worth of future cash flows in today's terms. Through this essay, we delve comprehensively into this fundamental concept, elucidating its technical terms and significance within financial valuation.
Time-Value of Money: The Essence
At the core of the present value of future cash flows lies the Time-Value of Money principle. This principle asserts that a sum of money today is worth more than the same sum in the future, due to the potential for investment and interest accumulation over time. As a result, future cash flows must be discounted to their present value to accurately reflect their economic value in today's context.
- The bedrock of the present value of future cash flows is the Time-Value of Money principle.
- This principle posits that the worth of money today surpasses its worth in the future due to investment potential and interest accrual.
- As a result, future cash flows must be adjusted or discounted to their current value to accurately represent their economic value in today's context.
Discounting for Value: Unraveling the Mechanism
- At the heart of the present value concept lies "discounting," a process that transforms future cash flows into their equivalent value today.
- The discount rate, a critical factor, encapsulates the interplay of risk and opportunity cost.
- It encompasses elements like the risk-free rate and a risk premium, accounting for uncertainty associated with investments.
- The choice of an appropriate discount rate is pivotal, as it shapes the valuation outcome.
Applications and Scenarios
-
Single Cash Flows:
- The concept applies straightforwardly to scenarios involving a single future cash flow.
- This technique aids in evaluating long-term investments or projecting the future value of lump-sum payments.
-
Structured Payments:
- Annuities, representing regular cash flows, and perpetuities, denoting infinite cash flows, fall within the ambit of this principle.
- Slight modifications to the formula accommodate these structured patterns.
-
Dynamic Patterns:
- In scenarios featuring growth or decline in cash flows, the concept of terminal value emerges.
- Terminal value captures the aggregate worth of all future cash flows beyond a certain point of stabilization.
-
Discounted Cash Flow Analysis (DCF):
- The cornerstone of the Discounted Cash Flow analysis, a prevalent valuation method.
- DCF involves summing the present values of all expected future cash flows to determine overall investment value.
Strategic Decision-Making
- The Present Value of Future Cash Flows holds immense implications for decision-making in various financial realms:
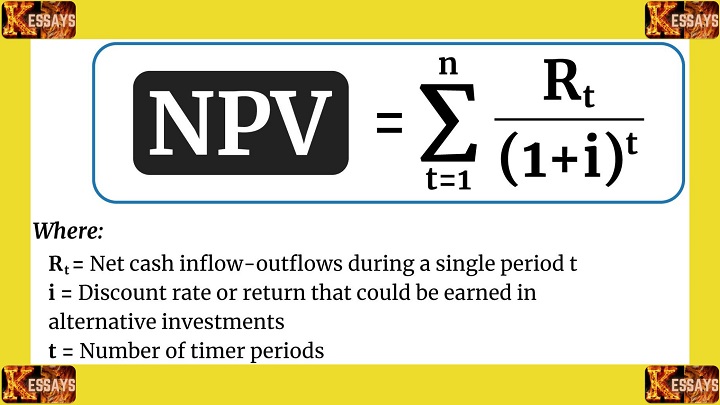
- Investment Evaluation: It aids in comparing potential investments by juxtaposing the present value of expected returns against the initial investment, guided by NPV calculations.
- Capital Allocation: Businesses leverage this concept for prudent resource allocation, comparing present values of anticipated cash flows with initial outlays for projects.
- Securities Valuation: It's pivotal in valuing fixed-income securities like bonds, aligning bond prices with the present value of future coupon payments and principal return.
- Risk Assessment: By adjusting the discount rate to accommodate higher risk, investors assess riskier ventures with a cautious approach, reflecting the risk-return trade-off.
- Financial Planning: Individuals employ this technique to shape savings, retirement, and education fund strategies, ensuring future financial needs are met.
Complexities and Considerations
- Despite its potency, the Present Value of Future Cash Flows isn't without limitations:
- Projection Uncertainty: Precise estimates of future cash flows and discount rates are imperative. Estimation errors can impact valuations significantly.
- Constant Discount Rate Assumption: The concept assumes a constant discount rate, which may not hold true in dynamic economic conditions.
- Intricate Patterns: Valuing complex cash flow patterns may necessitate advanced techniques like the Internal Rate of Return (IRR).
- Short-Term Bias: Overemphasizing short-term outcomes might overlook long-term investment opportunities with higher growth potential.
Discount Rate: Unraveling Risk and Opportunity
The discount rate, a pivotal element in the present value calculation, accounts for the risk and opportunity cost associated with waiting for future cash flows. It encompasses various components such as the risk-free rate, representing the return on a risk-free investment, and a risk premium, compensating for the additional risk inherent in an investment. The choice of an appropriate discount rate is paramount, as it shapes the valuation outcome.
Discount Rate: The Navigator of Value
- The discount rate is a linchpin in the present value calculation, steering the valuation process.
- It encapsulates two vital dimensions: risk and opportunity cost.
- The discount rate functions as a bridge between future cash flows and their present value, considering the time value of money.
Risk-Free Rate: Foundation of Safety
- One component of the discount rate is the risk-free rate.
- The risk-free rate signifies the return on a risk-free investment, usually represented by government bonds or other secure financial instruments.
- This rate serves as a baseline, reflecting the time value of money without the influence of risk.
Risk Premium: Navigating Uncertainty
- The second component, the risk premium, acknowledges the additional risk associated with investments beyond risk-free options.
- This premium compensates investors for taking on uncertainty and potential loss.
- It varies based on the investment type, industry, and market conditions, reflecting the perceived level of risk.
Balancing Act: Choosing the Appropriate Discount Rate
- Selecting the right discount rate is paramount, as it shapes the valuation outcome.
- A higher discount rate indicates a more cautious approach, reflecting greater perceived risk and requiring higher returns to justify the investment.
- A lower discount rate, on the other hand, suggests a more optimistic outlook, accommodating a higher present value for future cash flows.
Practical Implications: Affecting Valuation Outcomes
- The choice of the discount rate profoundly impacts investment decisions.
- Investments with higher risk levels demand a higher discount rate, resulting in lower present values.
- Conversely, less risky investments have lower discount rates, leading to higher present values.
Complexities and Considerations
- Determining the appropriate discount rate is not without challenges.
- It requires a nuanced understanding of the investment's risk profile, market conditions, and other influencing factors.
- Overestimating or underestimating the discount rate can lead to misaligned valuations.

Present Value Formula: Mathematical Expression
The mathematical expression for calculating the present value of future cash flows is as follows:
PV = FV / (1 + r)^n
Where:
- PV = Present Value of the future cash flow
- FV = Future Value of the cash flow
- r = Discount Rate
- n = Number of periods
This formula captures the essence of discounting future cash flows to their current value, considering the discount rate and the time horizon.
Components of Present Value Analysis
- Single Cash Flow: In scenarios involving a single future cash flow, the present value can be determined straightforwardly using the formula. This technique finds application in assessing the desirability of long-term investments or evaluating the future worth of lump-sum payments.
- Annuities and Perpetuities: An annuity refers to a series of regular cash flows, while perpetuities represent infinite cash flows at regular intervals. Both concepts extend the present value calculation to these structured payment patterns, involving slight modifications to the formula.
- Growth and Decline Scenarios: In cases where the future cash flows exhibit growth or decline patterns, such as in business projections, the concept of terminal value comes into play. Terminal value captures the value of all future cash flows beyond a certain point, typically when they stabilize.
- Discounted Cash Flow (DCF) Analysis: Present value of future cash flows serves as the cornerstone of the Discounted Cash Flow analysis, a widely used valuation method in finance. DCF involves summing up the present values of all future expected cash flows to ascertain the overall value of an investment.
Significance in Decision Making
The present value of future cash flows plays a pivotal role in aiding decision-making across various financial scenarios:
- Investment Valuation: It facilitates the evaluation of potential investments by comparing the present value of expected returns against the initial investment. This enables investors to discern whether an investment is worthwhile based on the net present value (NPV) calculation.
- Capital Budgeting: Businesses employ present value analysis to assess the feasibility of capital-intensive projects. By comparing the present value of expected cash inflows with initial outlays, organizations can make informed decisions about resource allocation.
- Securities Valuation: The concept is crucial in valuing fixed-income securities like bonds. Investors determine the fair price of a bond by discounting its future coupon payments and principal repayment.
- Risk Assessment: Incorporating a higher discount rate to reflect higher risk factors aids in evaluating riskier ventures more cautiously, aligning with the concept of risk-return trade-off.
- Financial Planning: Individuals employ present value calculations to make prudent decisions regarding savings, retirement planning, and education funds. It helps individuals gauge the sufficiency of their financial resources for future needs.
Challenges and Limitations
While the present value of future cash flows is a powerful tool, it comes with inherent challenges and limitations:
- Estimation Uncertainty: Accurate valuation relies on precise estimates of future cash flows and an appropriate discount rate. These estimations can be subject to errors, impacting the reliability of the valuation.
- Constant Discount Rate Assumption: The concept assumes a constant discount rate over time, which might not hold true in dynamic economic environments.
- Complex Cash Flow Patterns: Valuing intricate cash flow patterns can be complex, necessitating the use of advanced techniques like the Internal Rate of Return (IRR) and modified present value calculations.
- Short-Term Focus: Excessive focus on short-term outcomes might lead to undervaluing long-term investments with higher growth potential.

Conclusion
The present value of future cash flows is a bedrock concept in finance, underpinning the assessment of investment viability and facilitating informed decision-making. Its integration with the Time-Value of Money principle provides a systematic framework for evaluating the worth of future cash flows by considering the factors of time and risk. By employing this concept, individuals and businesses can navigate the intricate landscape of financial valuation, empowering themselves to make optimal choices amidst uncertainty and opportunity.



Comments are closed!