Introduction

Accurately valuing an investment requires more than forecasting short-term cash flows. It demands a clear understanding of how long-term value is created and sustained. One of the most critical concepts used to capture this long-term economic potential is the Present Value of Terminal Value, a core component of financial valuation and Discounted Cash Flow analysis.

Because most businesses are expected to operate indefinitely, it is neither practical nor reliable to project cash flows year by year into perpetuity. Terminal Value addresses this limitation by estimating the value of all future cash flows beyond the explicit forecast period and discounting them back to their present value. In many valuations, this single component represents a substantial share of total enterprise value, making its correct estimation essential for sound financial analysis.

This article examines the Present Value of Terminal Value by explaining its meaning, its importance in valuation models, the methods used to calculate it, and its practical applications across investment analysis, corporate finance, and asset valuation.

What Is the Present Value of Terminal Value

Definition of Present Value of Terminal Value

The Present Value of Terminal Value is the discounted value of all future cash flows that occur after the final year of a financial forecast. It is used to estimate the long-term value of a business or investment beyond the explicit projection period. This concept is fundamental in valuation because most businesses are assumed to continue operating and generating cash flows indefinitely.

Terminal Value in Discounted Cash Flow Analysis

Terminal Value in DCF represents the value of an investment at the end of the forecast period before discounting. Since Discounted Cash Flow analysis is based on present value principles, Terminal Value must be converted into today’s value to be comparable with forecasted cash flows. This is achieved by discounting the Terminal Value using the same discount rate applied throughout the DCF model.

Terminal Value Formula and Present Value Adjustment

The Terminal Value formula estimates future value at the end of the forecast horizon, while the Present Value of Terminal Value formula discounts that estimate back to the present. This two-step process ensures that long-term cash flows are properly aligned with current valuation standards. Without discounting, Terminal Value would overstate the true economic value of future cash flows.

Present Value of Terminal Value Perpetuity Formula

When cash flows are assumed to grow at a constant rate indefinitely, the Present Value of Terminal Value perpetuity formula is commonly applied. This approach is suitable for stable businesses with predictable long-term growth. It allows analysts to summarize infinite future cash flows into a single present value figure.

Terminal Value Example in Valuation

A Terminal Value example typically involves estimating cash flow in the final forecast year, applying the appropriate Terminal Value formula, and then discounting the result to the present. This example demonstrates how Terminal Value often represents a large portion of total enterprise value, highlighting the importance of accurate assumptions in long-term valuation.

Interpreting the Present Value of Terminal Value

In practical terms, Terminal Value answers what a business is worth after the forecast period, while the Present Value of Terminal Value explains what that future worth is worth today. Understanding this distinction is essential for accurate financial valuation, investment analysis, and strategic decision-making.

Read Also: The Role of Terminal Value in Financial Modeling

Importance of Terminal Value in Discounted Cash Flow Analysis

Capturing Long Term Cash Flows in DCF

Most investments continue generating cash flows long after the formal forecast period ends. Terminal Value in DCF ensures that these long term cash flows are included in the valuation. Without Terminal Value, a Discounted Cash Flow model would only measure short term performance and ignore a large portion of the investment’s economic value. This is especially important for established businesses with predictable cash flows.

Reflecting Ongoing Business Growth

Businesses do not usually stop operating when the forecast period ends. They often continue growing due to factors such as market expansion, efficiency improvements, and brand strength. The Terminal Value formula allows analysts to account for this ongoing growth by assuming a stable growth rate beyond the forecast period. When using the Present Value of Terminal Value perpetuity formula, future growth is captured in a structured and realistic way.

Ensuring Valuation Completeness

A complete Discounted Cash Flow valuation has two components. The first is the present value of forecasted cash flows. The second is the Present Value of Terminal Value. Excluding Terminal Value would understate the true value of the investment because it would ignore all cash flows beyond the forecast horizon. In many cases, the Present Value of Terminal Value represents the largest portion of total enterprise value.

Improving Accuracy Through Proper Discounting

Terminal Value is calculated at the end of the forecast period using a Terminal Value formula. To make it meaningful for today’s decision making, it must be discounted back to the present using the Present Value of Terminal Value formula. This step ensures consistency with time value of money principles and prevents overestimating future cash flows.

Supporting Informed Financial Decisions

Accurate estimation of Terminal Value helps investors and analysts make better financial decisions. By using a clear Terminal Value example or Present Value of Terminal Value example, students can see how long term assumptions affect valuation outcomes. This understanding improves investment comparisons, acquisition pricing, and assessments of whether an asset is undervalued or overvalued based on its long term cash flow potential.

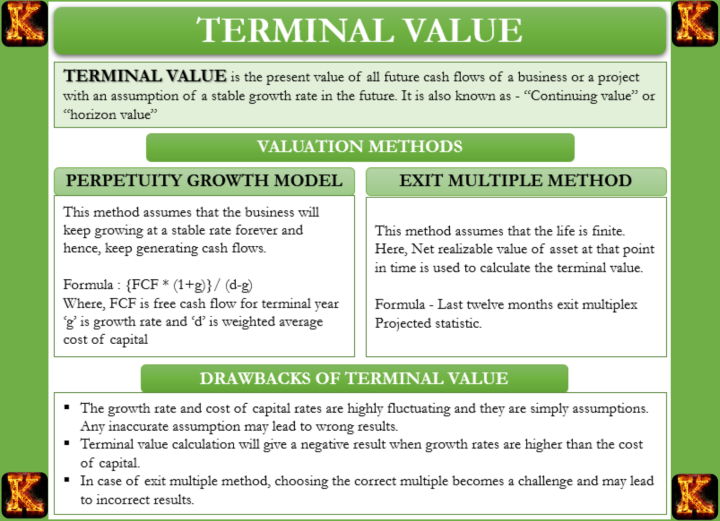
Methods for Calculating Terminal Value

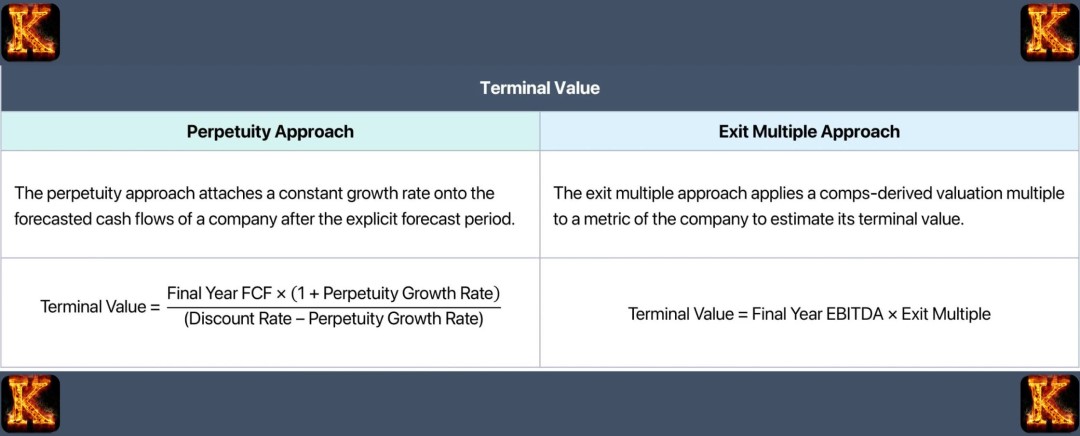
Terminal Value in DCF is estimated using assumptions about how a business performs after the forecast period. Two commonly used methods are the Perpetuity Growth Model and the Exit Multiple Method. Each method answers the same question but uses a different logic.

Perpetuity Growth Model

Key idea

The Perpetuity Growth Model assumes that a business will continue generating cash flows forever and that those cash flows will grow at a constant and stable rate.

Why this method is used

This approach is appropriate for mature and stable businesses where long term growth is expected to be steady and predictable. It is commonly used when applying the Present Value of Terminal Value perpetuity formula in Discounted Cash Flow analysis.

Terminal Value formula

Terminal Value formula:

Terminal Value = Final Year Cash Flow × (1 + g) ÷ (r − g)

Where:

• Final Year Cash Flow is the cash flow in the last forecast year

• g is the perpetual growth rate

• r is the discount rate

The growth rate should be conservative and usually close to long term economic growth.

Terminal Value Example Using the Perpetuity Growth Model

Assumptions

Final Year Cash Flow = 100,000
Perpetual Growth Rate g = 3 percent
Discount Rate r = 10 percent

Step 1: Calculate Terminal Value

Terminal Value = 100,000 × (1 + 0.03) ÷ (0.10 − 0.03)
Terminal Value = 103,000 ÷ 0.07
Terminal Value = 1,471,429

This amount represents the value of all future cash flows at the end of the forecast period.

Step 2: Apply the Present Value of Terminal Value Formula

If the forecast period ends in Year 5, the Present Value of Terminal Value is calculated by discounting the Terminal Value back to today using the discount rate.

This step produces the Present Value of Terminal Value used in the DCF model.

Exit Multiple Method

Key idea

The Exit Multiple Method estimates Terminal Value by assuming the business is sold at the end of the forecast period based on market valuation multiples.

Why this method is used

This method reflects how similar companies are valued in the market. It is commonly used when reliable market comparables are available.

Terminal Value Formula Using Exit Multiple

Terminal Value formula:

Terminal Value = Final Year Metric × Selected Multiple

Common metrics include EBITDA, earnings, or revenue. The selected multiple should be based on comparable companies or industry benchmarks.

Terminal Value Example Using the Exit Multiple Method

Assumptions

Final Year EBITDA = 200,000
Selected EBITDA Multiple = 6

Calculation

Terminal Value = 200,000 × 6
Terminal Value = 1,200,000

This value represents the estimated market value of the business at the end of the forecast period.

Choosing the Appropriate Method

The Perpetuity Growth Model focuses on long term cash flow sustainability, while the Exit Multiple Method reflects market based valuation. In practice, analysts often calculate Terminal Value using both methods and compare results to ensure the valuation is reasonable and consistent.

Read Also: Present Value of Future Cash Flows

Discounting Terminal Value to Present Value

Why Terminal Value Must Be Discounted

Terminal Value in DCF is calculated at the end of the forecast period, not today. Because money received in the future is worth less than money received today, Terminal Value must be converted into present value terms. This is done using the Present Value of Terminal Value formula. Discounting ensures that future cash flows are measured consistently with the time value of money principle.

Role of the Discount Rate in Terminal Value

The discount rate represents the risk of the investment and the required rate of return. In corporate valuation, this rate is commonly the Weighted Average Cost of Capital. Using the same discount rate for both forecasted cash flows and Terminal Value ensures consistency within the Discounted Cash Flow model.

Present Value of Terminal Value Formula

The Present Value of Terminal Value formula is:

Present Value of Terminal Value = Terminal Value ÷ (1 + r)ⁿ

Where:

• Terminal Value is the value calculated at the end of the forecast period

• r is the discount rate

• n is the number of years in the forecast period

This formula converts the future Terminal Value into its value today.

Present Value of Terminal Value Example

Step 1: Identify the Terminal Value

Assume the Terminal Value calculated using a Terminal Value formula is 1,500,000 at the end of Year 5.

Step 2: Identify the Discount Rate and Time Period

Discount Rate r = 10 percent
Number of Years n = 5

Step 3: Apply the Present Value of Terminal Value Formula

Present Value of Terminal Value = 1,500,000 ÷ (1 + 0.10)⁵
Present Value of Terminal Value = 1,500,000 ÷ 1.61051
Present Value of Terminal Value ≈ 931,000

This amount represents the value today of all cash flows beyond the forecast period.

Importance of Discounting Terminal Value Correctly

Discounting Terminal Value correctly is critical because it often represents a large portion of total enterprise value. Even small changes in the discount rate or forecast period can significantly affect valuation results. Understanding this step helps students build accurate DCF models and avoid overstating long term investment value.

Practical Applications of Terminal Value

Business and Enterprise Valuation

Terminal Value is a core component of business and enterprise valuation, especially in mergers and acquisitions. When valuing a company using Terminal Value in DCF, analysts estimate cash flows for a limited forecast period and then use a Terminal Value formula to capture all future earnings beyond that period. This ensures that the valuation reflects the full economic life of the business.

Example

A company is forecast to generate cash flows for five years. After Year 5, a Terminal Value example is calculated using the perpetuity growth approach. The Present Value of Terminal Value is then added to the present value of forecasted cash flows to estimate total enterprise value. This figure guides acquisition pricing and negotiation decisions.

Equity and Investment Analysis

Equity analysts rely on Terminal Value to estimate the intrinsic value of a company’s shares. Since most companies are expected to operate indefinitely, Terminal Value often represents a large portion of the Present Value of Terminal Value in equity valuations. This helps analysts determine whether a stock is undervalued or overvalued.

An analyst builds a DCF model for a listed company. After projecting cash flows for ten years, a Terminal Value is calculated and discounted using the Present Value of Terminal Value formula. The total firm value is divided by the number of shares outstanding to estimate intrinsic share price.

Infrastructure and Project Finance

Infrastructure projects generate cash flows over long periods, often several decades. Terminal Value in DCF is used to capture operating cash flows beyond the initial project forecast. This is critical for assessing project viability and attracting long term financing.

A power plant is forecast to operate for 25 years. Cash flows are projected for the first 10 years, after which a Terminal Value formula is applied. The Present Value of Terminal Value is included in the valuation to reflect ongoing electricity sales and long term revenue stability.

Real Estate Valuation

Real estate assets such as rental apartments and commercial buildings produce income over extended periods. Terminal Value helps estimate the future value of rental income beyond the explicit forecast period and is commonly used in property DCF models.

An investor forecasts rental income for a commercial building for seven years. A Terminal Value example is calculated based on stable long term rental growth. The Present Value of Terminal Value is added to discounted rental cash flows to estimate the property’s market value.

Why Terminal Value Matters in Practice

Across business valuation, investment analysis, infrastructure finance, and real estate, Terminal Value ensures that long term cash flows are not ignored. Understanding how to apply Terminal Value and the Present Value of Terminal Value formula allows students to produce realistic and complete valuations in academic and professional settings.

Conclusion

The Present Value of Terminal Value is a fundamental concept in financial valuation because it captures the value of cash flows that occur after the forecast period. Since most businesses and investments continue operating well into the future, Terminal Value in DCF ensures that long term performance is properly included rather than ignored.

By learning how to apply the Terminal Value formula, the Present Value of Terminal Value formula, and the Present Value of Terminal Value perpetuity formula, students can build valuation models that are complete and realistic. Understanding Terminal Value examples and how discounting works helps improve accuracy in business valuation, investment analysis, and project evaluation. Mastery of this concept is essential for anyone studying or working in finance, corporate valuation, or investment decision making.

Read Also: Present Value of Future Cash Flows