Introduction
In finance, the concept of the present value of future cash flows serves as a cornerstone for evaluating the true worth of investments, projects, and financial securities. The principle is grounded in the Time Value of Money (TVM), which asserts that a sum of money available today is more valuable than the same amount received in the future because of its potential earning capacity. By applying present value analysis, individuals, firms, and policymakers can translate expected future cash inflows or outflows into their equivalent value today.
This approach provides a systematic framework for comparing different investment opportunities, determining the fair value of assets, and assessing whether a project will generate returns that exceed its costs. It is particularly relevant in capital budgeting, stock and bond valuation, and corporate finance decisions. Key technical elements include discounting, which involves applying a discount rate to future cash flows, and the consideration of risk, inflation, and opportunity cost when selecting the appropriate rate.
The significance of present value calculations extends beyond theoretical finance. Businesses rely on this method to decide whether to undertake new ventures, expand operations, or acquire competitors. Investors use it to evaluate whether a stock is undervalued or overpriced based on projected dividends and earnings. Governments and policymakers apply it in cost-benefit analyses of public projects. By capturing both the timing and risk of cash flows, present value ensures that financial decisions are made on a realistic, data-driven basis rather than on raw future amounts that may appear attractive but lack contextual meaning.
Time-Value of Money: The Essence
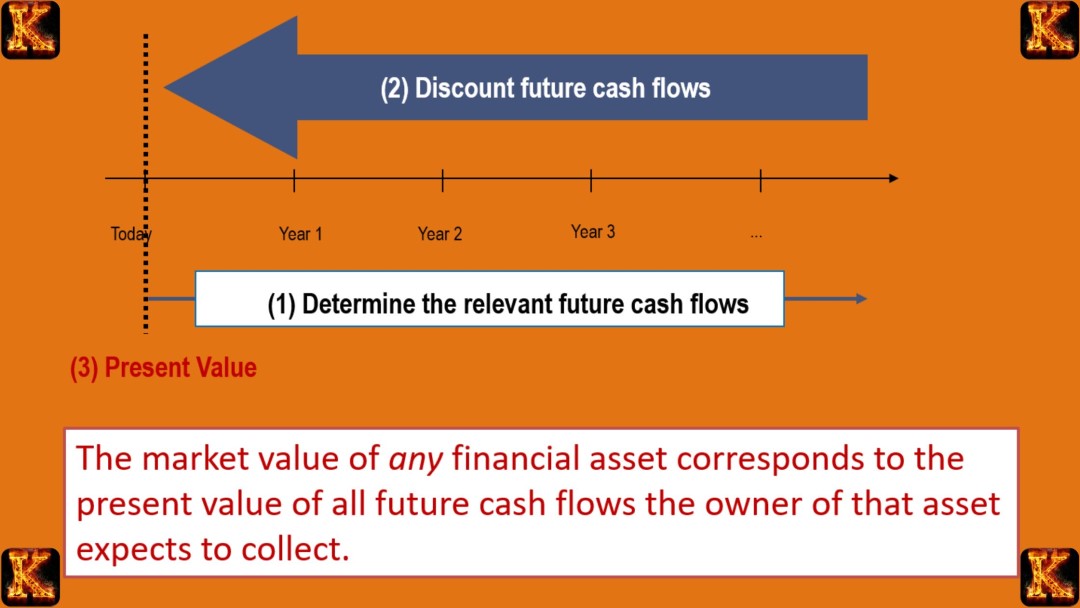
The foundation of the present value of future cash flows is the Time-Value of Money (TVM) principle. This principle explains that money available today is more valuable than the same amount received in the future. The reason is that money held now can be invested to earn interest, generate returns, or be used for opportunities that may not exist later.
Because of this, future cash flows must be discounted to their present value in order to represent their true worth in today’s terms. This adjustment prevents financial analysis from being based on inflated figures that ignore the effects of time and uncertainty.
Discounting for Value: Unraveling the Mechanism
At the heart of present value calculations is the process of discounting. This mechanism translates future amounts into their equivalent value today.
How it works:
-
The discount rate is applied to future cash flows. This rate reflects the time value of money, the opportunity cost of capital, and the risks tied to the investment.
-
The rate usually combines a risk-free component (such as the return on government securities) with a risk premium to account for uncertainty.
-
The choice of discount rate significantly influences the valuation outcome. A higher rate reduces the present value of future returns, while a lower rate increases it.
Applications and Scenarios
The present value concept applies to different financial settings, ranging from simple to complex.
Single Cash Flows
When there is a one-time payment or receipt expected in the future, present value helps determine what that amount is worth today. For example, a promise to receive $10,000 in five years will not hold the same value now once discounted.
Structured Payments
In many cases, cash flows are spread out over time. Annuities represent regular payments over a fixed period, such as retirement benefits or mortgage installments. Perpetuities, on the other hand, represent continuous cash flows with no end, such as dividends on certain types of stocks. Both can be valued by adapting the present value formula.
Dynamic Cash Flow Patterns
In real business environments, cash flows may not remain constant. They might grow or decline depending on circumstances. To handle this, analysts use terminal value, which estimates the total value of future cash flows beyond a specific forecast horizon. This is particularly useful for valuing companies with long-term growth potential.
Discounted Cash Flow (DCF) Analysis
Perhaps the most widely known application of present value is in DCF analysis. Here, all expected cash flows from an investment are forecast, discounted back to their present value, and then summed up to determine the intrinsic value of the project or company.
Strategic Decision-Making
Understanding the present value of future cash flows has significant implications for financial decision-making. Investors rely on it to assess whether a project or asset will yield adequate returns. Businesses use it when allocating capital between competing projects. It plays a central role in the valuation of bonds, since bond prices are directly tied to the present value of coupon payments and principal repayment.
Risk assessment also comes into play. By adjusting the discount rate upward for riskier ventures, analysts can reflect the balance between risk and reward. On a personal level, individuals use present value techniques in planning for retirement, education funding, or savings strategies, ensuring that today’s contributions align with tomorrow’s needs.
Complexities and Considerations
Despite its importance, the present value framework has limitations. The reliability of the results depends heavily on accurate projections of future cash flows and appropriate discount rates. Since both involve estimates, errors can significantly affect the outcome.
Another challenge is the assumption of a constant discount rate. Economic conditions, inflation, and market risks often fluctuate, which makes this assumption unrealistic in practice. Complex cash flow patterns may also require advanced tools such as the Internal Rate of Return (IRR) or stochastic modeling to capture variability.
Finally, there is the risk of short-term bias. Analysts and decision-makers may give more weight to immediate outcomes while undervaluing long-term opportunities. This can be particularly problematic in industries driven by innovation, where long-term investments often yield the greatest rewards.
Read Also: Project Selection Methods: NPV, IRR, & Payback Period
Discount Rate: Unraveling Risk and Opportunity
The discount rate is one of the most critical elements in present value calculations. It determines how future cash flows are translated into today’s terms, reflecting both the risk of uncertainty and the opportunity cost of tying up capital. By applying a discount rate, investors and businesses account for the fact that future money is less certain and less valuable than money in hand today.
Discount Rate as a Navigator of Value
The discount rate functions as a bridge between expected future returns and present value. It incorporates two essential dimensions:
-
The time value of money, which acknowledges that a dollar today is worth more than a dollar tomorrow.
-
The risk profile of the investment, which recognizes the chance of loss or underperformance.
This makes the discount rate a guiding tool in valuation, shaping whether an investment appears attractive or too risky.
Risk-Free Rate: The Baseline of Safety
One key component of the discount rate is the risk-free rate. This rate represents the return an investor could expect from a completely secure investment, typically tied to government bonds or other low-risk securities.
-
It reflects the pure time value of money with no risk adjustment.
-
It acts as the foundation on which all additional risk considerations are built.
For instance, if the risk-free rate is 3%, any investment must earn more than 3% to be worthwhile, since investors could otherwise achieve that return without exposure to risk.
Risk Premium: Accounting for Uncertainty
The second major component is the risk premium. This represents the additional return required to compensate investors for taking on uncertainty.
-
The size of the premium varies with the type of investment, the industry, and broader market conditions.
-
High-risk ventures such as startups or emerging market projects typically demand large premiums.
-
Stable investments such as established corporate bonds require smaller premiums.
The risk premium ensures that investors are rewarded for accepting the possibility of loss, volatility, or delayed returns.
Balancing Act: Choosing the Appropriate Discount Rate
Determining the correct discount rate is a balancing act.
-
Higher discount rates are applied when risk is high, which reduces the present value of future cash flows. This signals caution and demands higher returns to justify the investment.
-
Lower discount rates apply in more stable contexts, raising the present value of future cash flows and indicating greater confidence in the investment.
This decision can dramatically alter the outcome of a valuation, highlighting the importance of thoughtful judgment.
Practical Implications: Impact on Valuation
The choice of discount rate directly affects how investments are judged:
-
Riskier investments, such as speculative stocks or volatile projects, are discounted more heavily, resulting in lower present values.
-
Safer investments, such as government-backed securities or mature companies, are discounted at lower rates, making their future returns appear more valuable in present terms.
This mechanism allows analysts to compare investments fairly, taking both time and risk into account.
Complexities and Considerations
Despite its usefulness, setting the discount rate is not straightforward. It requires a nuanced understanding of both the investment environment and the broader economic context. Market conditions, inflation, industry volatility, and even investor sentiment can influence the decision.
Errors in estimating the discount rate can lead to flawed valuations:
-
Overestimating the rate undervalues future cash flows, possibly leading to the rejection of profitable opportunities.
-
Underestimating the rate inflates valuations, increasing the risk of investing in projects that may underperform.
As a result, financial professionals often use a range of discount rates in sensitivity analysis to test how different assumptions influence the outcome.

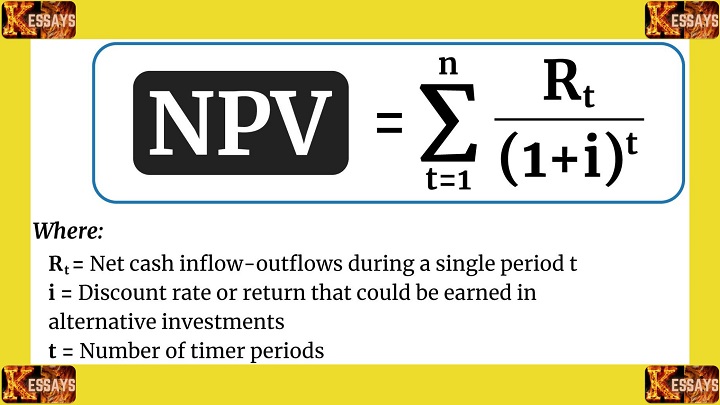
Present Value Formula: Mathematical Expression
The present value of future cash flows can be expressed mathematically through the following formula:
PV = FV / (1 + r)^nWhere:
-
PV = Present Value of the future cash flow
-
FV = Future Value of the cash flow
-
r = Discount rate
-
n = Number of periods until the cash flow occurs
This formula embodies the principle of discounting, which adjusts the value of a future sum by accounting for the time value of money and the level of risk. The further into the future the cash flow occurs, or the higher the discount rate applied, the lower its present value will be.
Components of Present Value Analysis
The basic formula adapts to different financial contexts, allowing analysts and decision-makers to evaluate a variety of scenarios:
Single Cash Flow
In its simplest form, present value applies to a single payment or receipt in the future. For example, the present value of $1,000 received five years from now can be computed directly by applying the discount rate over the specified period. This approach is often used for valuing lump-sum settlements or one-time investments.
Annuities and Perpetuities
Many financial situations involve a series of recurring cash flows. An annuity refers to regular payments over a fixed period, such as mortgage installments or pension benefits. A perpetuity refers to infinite recurring payments, such as certain preferred stock dividends. Both extend the present value framework, with formulas that account for the structured pattern of payments.
Growth and Decline Scenarios
Cash flows are rarely static. Businesses may project growth or decline in future revenues and expenses. In such cases, the concept of terminal value becomes important. Terminal value estimates the worth of all future cash flows beyond a forecast horizon, usually once growth stabilizes. This is a key feature of long-term business valuations.
Discounted Cash Flow (DCF) Analysis
Discounted cash flow analysis is one of the most widely used applications of present value. It involves summing the present values of all expected cash flows to determine the intrinsic value of an investment, company, or project. DCF is central in corporate finance, mergers and acquisitions, and equity valuation.
Significance in Decision-Making
The present value of future cash flows is not just a theoretical concept. It plays a central role in practical decision-making across personal, corporate, and institutional finance.
-
Investment Valuation: By comparing the present value of expected returns with the initial cost, investors determine whether an investment creates value. This is the basis of net present value (NPV) calculations.
-
Capital Budgeting: Companies use present value analysis to assess major projects such as factory expansions, product launches, or infrastructure investments. Comparing discounted inflows and outflows ensures efficient allocation of capital.
-
Securities Valuation: Bond pricing is fundamentally tied to present value, as investors calculate the worth of coupon payments and principal repayment. Equity valuation also applies PV concepts through dividend discount models and earnings projections.
-
Risk Assessment: Adjusting the discount rate for higher risk reflects the uncertainty of cash flows. This ensures that riskier projects are evaluated more cautiously and only pursued when potential rewards justify the exposure.
-
Financial Planning: Individuals use present value to plan for retirement, education expenses, or savings goals. It helps ensure that today’s contributions will be sufficient to meet future needs.
Challenges and Limitations
While powerful, present value analysis is not without shortcomings. The accuracy of the method depends heavily on the reliability of inputs and assumptions.
One challenge lies in estimation uncertainty. Forecasting future cash flows and selecting an appropriate discount rate involves assumptions that may be incorrect. Small errors in either factor can lead to significant misvaluations.
Another limitation is the constant discount rate assumption. Economic conditions rarely remain stable, yet present value calculations often assume that the discount rate remains fixed throughout the analysis. This can oversimplify reality in volatile markets.
Complex financial arrangements may also present difficulties. Intricate cash flow patterns, such as those found in projects with variable returns or contingent outcomes, require advanced techniques like the Internal Rate of Return (IRR) or modified present value models.
Finally, there is the risk of short-term focus. Analysts may undervalue investments with long-term growth potential if they place too much emphasis on near-term results. This bias can hinder investments in innovation or infrastructure that yield benefits far into the future.

Comments are closed!